原题链接

迷宫问题(方向数组int dir[4][1] = { {-1,0},{1,0},{0,-1},{0,1} };)

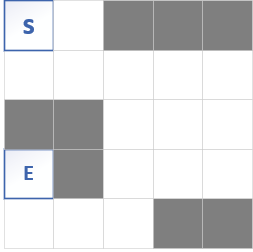
699kQ0.png
迷宫问题常用的两种解法DFS（优先深度遍历，先遍历纵，再遍历横）BFS(广度优先遍历，先遍历横，再遍历纵）

BFS(求最短路径长度）

![广度优先遍历流程图][2]

从起点开始每一个节点向可以延申的地方延申，最后走到终点，得到最短的路径长度，但是没有办法获得其路径。时间复杂度为o(n)为边长
```C++

include <bits/stdc++.h>

using namespace std;
struct point {
int x;
int y;
point(int x, int y)
{
this->x = x;
this->y = y;
}
};
int ex, ey;//终点坐标
int dir[4][3] = { {-1,0},{1,0},{0,-1},{0,1} };//方向数组
char Map[105][105];//地图
int vis[105][105] = { 0 };//记录是否访问，在bfs中记录每个点的步数
vectorres;
int ans = 0;//在dfs中是最短路径
int flag;
int m, n;//地图长宽
int FLAG = 0;
int Min = 0;
int quenex[10000];//这两个数组记录进队的点以及前驱节点
int queney[10000];
int front = 0, rear = 0;//队列的前驱和尾部

int BFS(int x, int y)
{
quenex[rear] = x;//起点入队，设其被拜访
queney[rear++] = y;
vis[x][y] = 1;
while (front != rear) {

    int nx = quenex[front];//前驱点坐标
    int ny = queney[front++];
    point* p = new point(nx, ny);//尝试记录每一个前驱点
    res.push_back(*p);
    if (nx == ex && ny == ey) { return vis[ex][ey] - 1; }//减去第一步
    for (int i = 0; i < 4; i++)//向四周尝试
    {
        int tx = nx + dir[i][0];
        int ty = ny + dir[i][4];
        if (tx >= 0 && ty >= 0 && vis[tx][ty] == 0 && Map[tx][ty] != '#' && tx < m && ty < n)//不撞墙不撞障碍
        {
            quenex[rear] = tx;
            queney[rear++] = ty;//将后面尝试成功的点入队
            vis[tx][ty] = vis[nx][ny] + 1;

        }
    }
}
return -1;

}
int main()
{
int N;
cin >> N;
int x, y;
while (N)
{
memset(&Map, '\0', sizeof(Map));
memset(&vis, 0, sizeof(vis));//题目要循环，每次重置数组，可以记一下如何重置二维数组
cin >> m >> n;
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
{
cin >> Map[i][j];
if (Map[i][j] == 'S')
{
x = i; y = j;

                vis[i][j] = 1;
            }
            if (Map[i][j] == 'E')
            {
                ex = i; ey = j;

            }

        }
    N--;
    cout << BFS(x, y) << endl;
    for (int i = 0; i < res.size(); i++)
        cout << '(' << res[i].x << ',' << res[i].y << ") ";
}

}

![BFS路径][5]



##DFS+回溯(可以找到最短路径，但时间复杂度贼高，图大了必过不了）

![第四到第五幅图因为走不通产生了回溯][6]

include <bits/stdc++.h>

using namespace std;
struct point {
int x;
int y;
point(int x, int y)
{
this->x = x;
this->y = y;
}
};
int ex, ey;//记录终点
int dir[4][7] = { {-1,0},{1,0},{0,-1},{0,1} };
char Map[105][105];
int vis[105][105] = { 0 };
vectorres;//路径上每一个点
vectoranw;//可能有多种到达方式，找到最小的路径
int ans = 0;
int flag;
int m, n;
int Min = 0;
void DFS(int x, int y)
{

if (x == ex && y == ey) { flag = 1; anw.push_back(ans); ans = 0; return; }
if (flag == 1)return;

for (int i = 0; i < 4; i++)
{
    int tx = x + dir[i][0];
    int ty = y + dir[i][8];
    if (tx >= 0 && ty >= 0 && vis[tx][ty] == 0 && Map[tx][ty] != '#' && tx < m && ty < n)
    {
        //记录下进入的点
        vis[tx][ty] += 1;
        ans++;
        point* p = new point(tx, ty);
        if (flag == 0)
        res.push_back(*p);

        DFS(tx, ty);
    //回溯
        vis[tx][ty] -= 1;
        if(flag==0)
        res.pop_back();
        ans--;
    }

}
return;

}

int main()
{
int N;
cin >> N;
int x, y;
while (N)
{
memset(&Map, '\0', sizeof(Map));
memset(&vis, 0, sizeof(vis));
cin >> m >> n;
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
{
cin >> Map[i][j];
if (Map[i][j] == 'S')
{
x = i; y = j;

                vis[i][j] = 1;
            }
            if (Map[i][j] == 'E')
            {
                ex = i; ey = j;

            }

        }
    N--;
    DFS(x, y);
    Min = anw[0];
    for (auto i = anw.begin(); i < anw.end(); i++)
    {
        if (Min < *i)Min = *i;
    }
    cout << Min<<endl;
    for (int i = 0; i < res.size(); i++)
        cout << '(' << res[i].x << ',' << res[i].y << ") ";
}

}


![DFS路径][9]

  [1]: https://s3.ax1x.com/2021/02/27/69pxeS.md.png
  [2]: https://s3.ax1x.com/2021/02/27/69pxeS.md.png
  [3]: https://s3.ax1x.com/2021/02/27/69pxeS.md.png
  [4]: https://s3.ax1x.com/2021/02/27/69pxeS.md.png
  [5]: https://s3.ax1x.com/2021/02/27/69iIXt.png
  [6]: https://s3.ax1x.com/2021/02/27/69PjL6.png
  [7]: https://s3.ax1x.com/2021/02/27/69pxeS.md.png
  [8]: https://s3.ax1x.com/2021/02/27/69pxeS.md.png
  [9]: https://s3.ax1x.com/2021/02/27/69i2kD.png